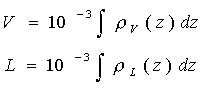 (1)
(1)
A MULTI-PARAMETER EMPIRICAL OCEAN ALGORITHM FORSSM/I
RETRIEVALS
Vladimir M. Krasnopolsky(1), William H. Gemmill and Laurence C. Breaker
Environmental Modeling Center
National Centers for Environmental Prediction
Washington, D.C. 20233
Submitted to Canadian Journal of Remote Sensing
January 1998
Revised and resubmitted to Canadian Journal of Remote Sensing
January 1999
Abstract
A new empirical multi-parameter SSM/I retrieval algorithm based on the neural network approach is introduced. This algorithm retrieves wind speed, columnar water vapor, columnar liquid water, and SST simultaneously using only SSM/I brightness temperatures. The new algorithm is compared with six existing global SSM/I wind speed retrieval algorithms. In terms of accuracy in retrieving wind speed, the new algorithm systematically outperforms all six algorithms under all weather conditions where retrievals are possible with an algorithm rms error of 1.0 m/s under clear, and 1.3 m/s under clear plus cloudy conditions. It also generates high wind speeds with acceptable accuracy. This improvement in accuracy is coupled with increased areal coverage, an obvious advantage for operational applications. In terms of columnar water vapor and columnar liquid water, the new algorithm reproduces the results of existing algorithms closely. SST retrievals are less accurate and have low spatial resolution; however, by including SST as an additional output, the accuracy in retrieving wind speed is improved especially at high wind speeds. In April 1998, the new algorithm was implemented operationally in the global data assimilation system at the National Centers for Environmental Prediction. Finally, this SSM/I retrieval algorithm illustrates a new generic approach, presented here for the first time, in developing a multi-parameter empirical retrieval algorithm based on neural networks. Because of its generality, this approach may find application in other areas of remote sensing as well.
List of Symbols-Notation
BT: brightness temperature
C: degrees Celsius
cal/val: calibration/validation
CC: correlation coefficient
F:
forward model
f: transfer
function
FXX: SSM/I instrument number XX
G: G
= {W, V, L, TS} - vector of geophysical parameters
GS: Goodberlet and Swift
(1992) - see References
GSW: Goodberlet, Swift and Wilkerson (1989) - see References
GSWP: GSW corrected by Petty (1993) - see References
L: columnar liquid water in mm
LIMA: European oceanic weather ship
MIKE: European oceanic weather ship
NCEP: National Centers for Environmental Prediction
NDBC: National Data Buoy Center
NN: neural network
OMBNNX: Ocean Modeling Branch Neural Network (version) X - SSM/I
NN retrieval algorithms, version X
PB: physically-based
Rn: n-dimensional linear vector space
SD: standard deviation
SSM/I: Special Sensor Microwave / Imager
tanh: hyperbolic tangent
Tv,p
orT:
vector
of SSM/I BTs
TS, SST: sea surface temperature
TAO: tropical atmosphere ocean
TOGA: tropical ocean global atmosphere
V: columnar water vapor in mm
W: wind speed in m/s
Introduction
We consider the problem of simultaneously retrieving several geophysical parameters over the ocean from the measurements acquired by the Special Sensor Microwave Imager (SSM/I) (Hollinger et al., 1987) with primary emphasis on retrieving wind speed. Five SSM/I sensors (F8, F10, F11, F13 and F14) have been successfully launched since 1987, and a significant amount of data have been collected from these instruments and subsequently matched to buoy observations. The SSM/I measures brightness temperatures (BTs) at four frequencies: 19.35,37, 85.5, (vertical and horizontal polarization), and 22.235 (vertical polarization only) GHz. From these channels it is possible to extract information concerning several geophysical parameters over the ocean including surface wind speed, W, columnar water vapor, V, columnar cloud liquid water, L, sea surface temperature, SST, rainfall, and ice concentration.
Here we consider the retrieval of three related parameters: W (m/sec), V (mm), and L (mm).Columnar water vapor and columnar cloud liquid water (in mm) can be defined as
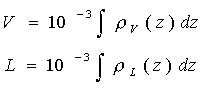 (1)
(1)
where V and L are water vapor and cloud liquid water densities (in g/m3) and the integrals are over height, z, (in m) from the surface to the top of the troposphere. We also retrieve SST as an auxiliary parameter which improves the retrieval accuracy of the primary parameter - wind speed; however, because the dependence of BT on SST is weak in the 19 to 37 GHz band, the retrieval accuracy for SST is low compared with SSTs retrieved, for example, from the AVHRR.
We present a new approach for deriving empirical retrieval algorithms based on the simultaneous retrieval of several parameters using the neural network (NN) technique. A new, multi-parameter empirical SSM/I retrieval algorithm(2) based on this approach is presented and compared with existing SSM/I retrieval algorithms. In April 1998, this new algorithm was implemented operationally in the global data assimilation system at NCEP. The wind speed, columnar water vapor, and columnar liquid water fields retrieved by this algorithm can be seen on our web site at: http://polar.ncep.noaa.gov/marine.meteorology/marine.winds.
In the next section we discuss various methods of producing satellite retrievals. Then the existing SSM/I global wind speed retrieval algorithms are reviewed and compared. Our approach for producing multi-parameter empirical retrievals is also introduced in this section. Next, a new multi-parameter NN-based SSM/I retrieval algorithm, OMBNN3, is introduced and compared with existing algorithms. In the Appendix we review different mathematical methods for performing empirical retrievals and introduce the NN technique as a generic tool for developing multi-parameter empirical algorithms.
Extracting Geophysical Parameters From Satellite Data
Conventional methods of deriving geophysical parameters from satellite data require the solution of an inverse (i.e., retrieval) problem to derive a transfer function (TF), f, which relates the geophysical parameters of interest, G (ocean surface and atmospheric parameters), to a set of satellite measurements, T ,
G = f (T) (2)
The TF, f,
may be derived explicitly or assumed implicitly; it is usually nonlinear.
Relation (2) may be considered as a continuous mapping which maps a vector
of sensor measurements, T = {Tv,p}
in
Rn
(n is
frequency, p is
polarization) to a vector of geophysical parameters G = {gi}
in
Rm.
In the case of the SSM/I, T is a vector of SSM/I BTs and
G
includes W, V, L, and TS (SST).
Physically-based retrieval algorithms
A retrieval algorithm is a particular representation for TF (2). A physically-based retrieval algorithm represents an inversion of a physically-based forward model. Physically-based SSM/I retrieval algorithms (Wentz, 1992, 1997) use algebraic versions of the radiative transfer forward model
![]() (3)
(3)
where Tv,p
is
the channel BT ( is frequency, is polarization); ![]() is
the upwelling atmospheric BT;
is
the upwelling atmospheric BT; ![]() is
the downwelling atmospheric BT;
is
the downwelling atmospheric BT; ![]() is sea surface emissivity;
is sea surface emissivity; ![]() is
atmospheric transmittance;
is
atmospheric transmittance;![]() is sea surface roughness, TS is SST, and TBC
= 2.7 K is the cosmic background radiation temperature. Symbolically, this
forward model can be written as
is sea surface roughness, TS is SST, and TBC
= 2.7 K is the cosmic background radiation temperature. Symbolically, this
forward model can be written as
![]() (4)
(4)
where G = {gi} = {W, V, L, TS}.
Now, the forward model (4) can be inverted (an inverse problem must be solved) to obtain the TF as in (2). In the most favorable case, the forward model can be inverted explicitly in the complete parameter space and the solution (2) provides the complete vector of parameters G simultaneously. In the case of the SSM/I, the forward model (3) can not be inverted explicitly. Numerical iterative inversion has been applied (Wentz, 1992, 1997) which is based on the linearization of the forward model (4) where
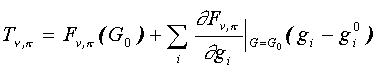 (5)
(5)
in the vicinity of vector G0 = {gi0} = {W0, V0, L0, TS0} that is assumed to approximate the true solution of the inverse problem, G. Then eq. (5) is a good approximation for (3, 4) and can be solved with respect to a small increment in G, G = {gi} = G - G0,
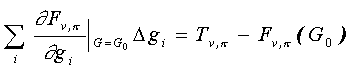 (6)
(6)
The solution, G, gives a new approximation for the solution of the inverse problem, G G0(1) = G0 + G, and eqs. (6) are solved with G0(1) used in place of G0, and so on, until convergence is reached. This procedure does not provide an explicit TF; however, if it converges, it provides an algorithm for retrieving a complete set of geophysical parameters from SSM/I brightness temperatures or a "simultaneous multi-parameter retrieval algorithm". Unfortunately, as mentioned above, the SSM/I was not designed to retrieve SST and, as a result, the iterative procedure (6) converges very slowly (or does not converge) with respect to TS. Therefore, to develop a retrieval algorithm based on this procedure, SST must be provided externally (Wentz, 1992, 1997). Then, the TF implicitly provided by such a retrieval procedure can be written symbolically as,
G = f (T, TS ) (7)
where G
= {W, V, L}. Thus, eq. (7) represents a partial, multi-parameter,
physically-based retrieval scheme (only three out of the four relevant
geophysical parameters are retrieved) where the fourth parameter, SST,
is required as an additional input.
Empirical retrieval algorithms: single- vs. multi-parameter retrievals.
Empirical algorithms
are based on a statistical approach that assumes an explicit analytic representation
for TF, f, which may be a complicated, nonlinear function.
A particular mathematical model, fmod, is usually
chosen (e.g., regression- or NN-based, see Appendix) which contains a vector
of model coefficients a = {a1, a2,
...},
G = fmod (T, a )
(8)
These coefficients are estimated empirically from a matchup set of observations {G , T } using statistical techniques such as the method of least-squares.
Most SSM/I retrieval algorithms are single-parameter and empirical; they retrieve only wind speed (Goodberlet et al., 1989), water vapor (Alishouse, 1990; Petty, 1993), or cloud liquid water (Weng and Grody, 1994; 1997), etc. Single-parameter retrieval algorithms may be represented as (here we consider the retrieval of SSM/I wind speed)
w = f (T,a) (9)
This representation contains hidden assumptions which may cause the wind speed, w, retrieved by a single-parameter algorithm (9) to differ significantly from the instantaneous surface wind speed, W, retrieved by a multi-parameter, physically-based algorithm (7). We trace the path from (7) to (9) to identify the assumptions which are made.
The first step in proceeding from (7) to (9) is to remove water vapor, V, and liquid water, L, from the vector of retrievals, G, but introduce them as additional arguments which we must now specify from external sources,
W = f (T,V,L,TS) = f (T,G') (10)
where G' = {gi}i=1,2,3 = {V, L,TS}
Proceeding from (10) to (9) involves removing the dependencies on V, L, and TS . Let us introduce a model for (10) which separates the T, V, L, and TS dependencies through a Taylor series expansion, and, assuming for simplicity that f is approximately linear,consider only the first two terms,
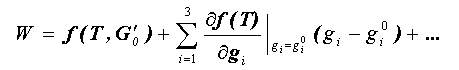 (11)
(11)
where G0 = {g0i}i=1,2,3 are the mean values for V, L, and TS.. The first term in (11) depends on BT only, and can be identified with the single-parameter retrievals w in (9). To estimate the difference between the instantaneous wind speed W retrieved by the multi-parameter algorithm, and the wind speed w retrieved by a single parameter algorithm, we now calculate the mean difference (bias), b, between these retrievals (W -w), and the standard deviation, , of the differences, by averaging over V, L, and TS.,
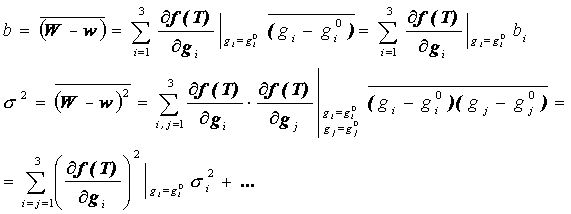 (12.1)
(12.1)
(12.2)
Horizontal bars above the symbols denote averaging over V, L, and TS; bi and si2 are the bias and variance of the geophysical parameter gi. It is clear from (12) that the transition from multi-parameter to single-parameter retrievals even in this favorable situation (when f is approximately linear) introduces additional "artificial" systematic (bias, b) and random (unaccounted variance s2) errors in wind speed, w, retrieved by a single-parameter algorithm (9). Only under ideal conditions can b = 0 in (12.1), and s2 (12.2) will never be equal to zero.
In the case of empirical algorithm development, this averaging occurs through our choice of matchup data. If, for each wind speed, W, the data contain events with all possible combinations of the other variables, V, L, and TS, then, in the above ideal case, the bias, b, may be zero. However, in reality, the matchup data are not necessarily representative, especially with respect to the availability of extreme values for W, V, L, and TS. Also, since f is usually nonlinear (which is true for the SSM/I), following terms in the expansion (11) must be taken into account. In this case, (12) becomes more complex and the "artificial" bias b is never zero.
Thus, single-parameter retrievals are usually biased and have higher random errors than corresponding multi-parameter retrievals. They produce retrievals with additional "artificial" systematic and random errors due to uncertainties in atmospheric and/or surface conditions which are related to the single retrieved parameter. In this case, the signatures (contributions to BT) of these related parameters, if not properly taken into account(3), act as additional sources of noise (pseudo noise) in the BT signal. As a result, (i), useful information about related geophysical parameters contained in these signatures is lost, and (ii), this pseudo noise causes additional errors in retrieving the parameter of primary interest, w. If the matchup data used for algorithm development spans the full dynamic range of wind speed, water vapor, etc., these additional "artificial" errors will contribute minimally to the bias, but they will still contribute to the scatter. However, for high values of wind speed, atmospheric moisture, etc., where the data are sparse, single-parameter algorithms will usually introduce a significant bias and a higher scatter for the estimated parameter w. This error, for example, contributes significantly to errors in retrieving wind speed at high wind speeds.
The obvious way to
improve upon single-parameter retrievals (9) is to include the other parameters
in the retrieval process, using the empirical multi-parameter approach
which, as in the physically-based multi-parameter approach (4-6), inverts
the data in the complete space of geophysical parameters. Thus, the complete
vector of related geophysical parameters is retrieved simultaneously from
the same vector of BTs:
G =
fmod(T, a)
(13)
where G
= {W,V,L,TS} is now a vector which contains the primary,
physically-related, atmospheric and ocean surface parameters which contribute
to the observed SSM/I BTs. These retrievals do not contain the additional
"artificial" systematic and random errors just described. Because eq. (13)
represents a continuous mapping, the NN technique is well suited for constructing
fmod
(see Appendix ).
Physically-based vs. empirical retrievals.
The physically-based retrieval approach (4-7) has two primary advantages: (i) it provides additional insight into the physics of the problem; (ii) it produces multi-parameter retrievals or inversions in the complete parameter space(4), avoiding additional "artificial" systematic and random errors. On the other hand, it requires a physically-based forward model as a necessary prerequisite which is not required for empirical algorithm development. Also, empirical data are required to estimate the associated empirical coefficients in the physically-based forward model (3). For example, more than 35,000 matchups were useed to develop the physically-based algorithm by Wentz (1997), far greater than the number required to develop a corresponding empirically-based algorithm (see below). The physically-based algorithm (7) does not produce an explicit TF (a forward model must be inverted for each satellite measurement), plus it requires additional inputs (e.g., SST from climatology). Because climatological data can exhibit large differences from the true atmospheric and ocean surface states, eq. (7) can yield significant retrieval errors for SSM/I-derived geophysical parameters such as wind speed. Overall, the resulting retrieval accuracies for the physically-based algorithms are often comparable to the accuracies obtained using empirical algorithms but, in some cases, they may be lower (see next section).
Empirical algorithms are based on data inversion and do not require a physically-based forward model as a necessary prerequisite. They do require representative matchup data for their development. However, all empirical wind speed algorithms considered in this study (including the NN algorithm which is subsequently introduced) have been developed using data containing only 3,000 - 4,000 matchups. The single-parameter empirical approach suffers from additional "artificial" errors. The multi-parameter empirical retrieval approach (13), which simultaneously retrieves the entire vector of related geophysical parameters does not have this limitation. In this case, however, the matchup database which is required for algorithm development must be more comprehensive than for the single-parameter case, because it must contains information concerning additional geophysical parameters. However, this additional information about related parameters (V, L, and SST) is required only for training. After the training is complete, algorithm (13) uses only SSM/I BTs and does not require any additional information to produce retrievals for W, V, L, and SST.
Current Empirical SSM/I Wind Speed Retrieval Algorithms
In the previous section,
we described a physically-based (PB) SSM/I wind speed retrieval algorithm
(Wentz, 1997). Here we discuss several empirical SSM/I wind speed algorithms.
The single-parameter wind speed retrieval algorithm developed by Goodberlet
et al. (1989) (GSW) is a linear regression algorithm which is also linear
with respect to BT. It provides the following linear approximation for
the SSM/I TF
WGSW
= 147.9 + 1.0969 T19V - 0.4555 T22V - 1.76
T37V + 0.786 T37H (14)
Evaluation statistics for this algorithm are shown in Table 2 under GSW. Under clear conditions (Table 2), it retrieves wind speed with acceptable accuracy (RMS error of less than 2 m/s, and a low bias); however, under cloudy conditions where the amount of water vapor and/or cloud liquid water in the atmosphere increases, errors in wind speed increase significantly (Table 2) because the TF, f , becomes nonlinear. Even for clear conditions, when the amount of integrated water vapor is significant (e.g., in the tropics), the TF becomes nonlinear (Petty, 1993) and the accuracy of the GSW retrievals is reduced (Stogryn, et al., 1994) (also see Fig.2).
Goodberlet and Swift (1992) attempted to improve the performance of the GSW algorithm under cloudy conditions, using a single-parameter algorithm based on nonlinear regression which we refer to as GS,
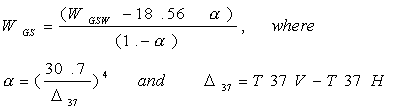 (15)
(15)
where WGSW is given by (14). Since the nature of the nonlinearity for the SSM/I TF under cloudy conditions is not known precisely, application of this nonlinear regression, as indicated in the Appendix, does not necessarily improve the results. In fact, this particular nonlinear relationship does not improve the retrieval accuracy even under clear conditions (Table 2) when compared with the linear GSW algorithm. Under cloudy conditions, the GS algorithm generates spurious high wind speeds. These fictitious high wind speeds occur in cases where the actual wind speeds are less than 15 m/s. The authors do not recommend using this algorithm when |T37V - T37H| < 40. K (Goodberlet and Swift, 1992); however, this limitation is not based on physical principles, but rather it arises from an inappropriate choice of the nonlinear regression function.
A single-parameter algorithm (GSWP), introduced by Petty (1993), is based on linear regression plus a nonlinear approximation technique (see Appendix). In the GSWP algorithm the nonlinearity (with respect to BT) is introduced in the linear regression, and represents more closely the nonlinear behavior of the TF due to increased water vapor concentration:
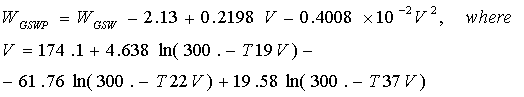 (16)
(16)
Here again, WGSW is given by (14), and a nonlinear function, -2.13 + 0.2198 V - 0.4008×10-2 V2 corrects the linear, single-parameter algorithm (14) for "artificial" variability of the wind speed due to changes in the concentration of water vapor (V).
NN algorithms have been introduced (Thiria, et al., 1993) as an alternative to nonlinear regression because they can model the nonlinear behavior of TFs without prior specification of any particular form of nonlinearity (see in Appendix). The first NN algorithm (SBB) for retrieving SSM/I wind speeds was developed by Stogryn et al. (1994) for retrieving a single parameter, wind speed, from SSM/I BTs. This algorithm consisted of two NNs, one which retrieves wind speed under clear conditions and a second which produced retrievals under cloudy conditions. Krasnopolsky et al. (1994, 1995a) showed that a single NN (OMBNN1) with identical architecture could generate retrievals with the same accuracy as the two NNs developed by Stogryn et al. for both clear and cloudy conditions. The OMBNN1 algorithm also led to a significant improvement in wind speed retrieval accuracy for clear conditions. For higher moisture/cloudy conditions which are generally of greater interest, the improvement was far greater (25-30%) compared to the GSW algorithm. The increase in areal coverage due to the higher retrieval accuracy of this algorithm was about 15% on average and even higher in areas of significant weather.
Both NN algorithms (SBB and OMBNN1) produce similar results because they have the same architecture and were developed using the same matchup database. This database, however, contains no matchups with wind speeds higher than about 20 m/s and few matchups higher than 15 m/s. Thus, not surprisingly, these NN algorithms demonstrate similar limited capabilities at high wind speeds. They are not able to generate wind speeds higher than 18 - 19 m/s. High wind speed accuracy is a critical factor in evaluating the performance of any wind speed retrieval algorithm. Unfortunately, high wind speed events are rare. Accurate measurements at high wind speeds are important for operational meteorology and for numerical weather prediction models. High wind speed performance has been improved in a second NN algorithm developed by Krasnopolsky et al. (1995b, 1996a), the OMBNN2 algorithm, by introducing new methods of NN training which enhance learning at high wind speeds, and by using a bias correction(5).
The OMBNN2 algorithm outperforms OMBNN1 (and SBB) for wind speeds higher than 15 m/s; however, it still can not generate wind speeds higher than 19 - 20 m/s without a bias correction because of the inherent limitations in the training set that was used. It is also a single-parameter algorithm and thus does not account for the variability of related atmospheric and surface parameters whose signatures are also contained in the BT signal. These single-parameter NN algorithms can be represented by eq. (A5- see Appendix) with q =1 (one output - wind speed, w) , k =2 (two hidden nods), and m = 4 (OMBNN1) or 5 (OMBNN2) (number of input BT channels, see Table 1).
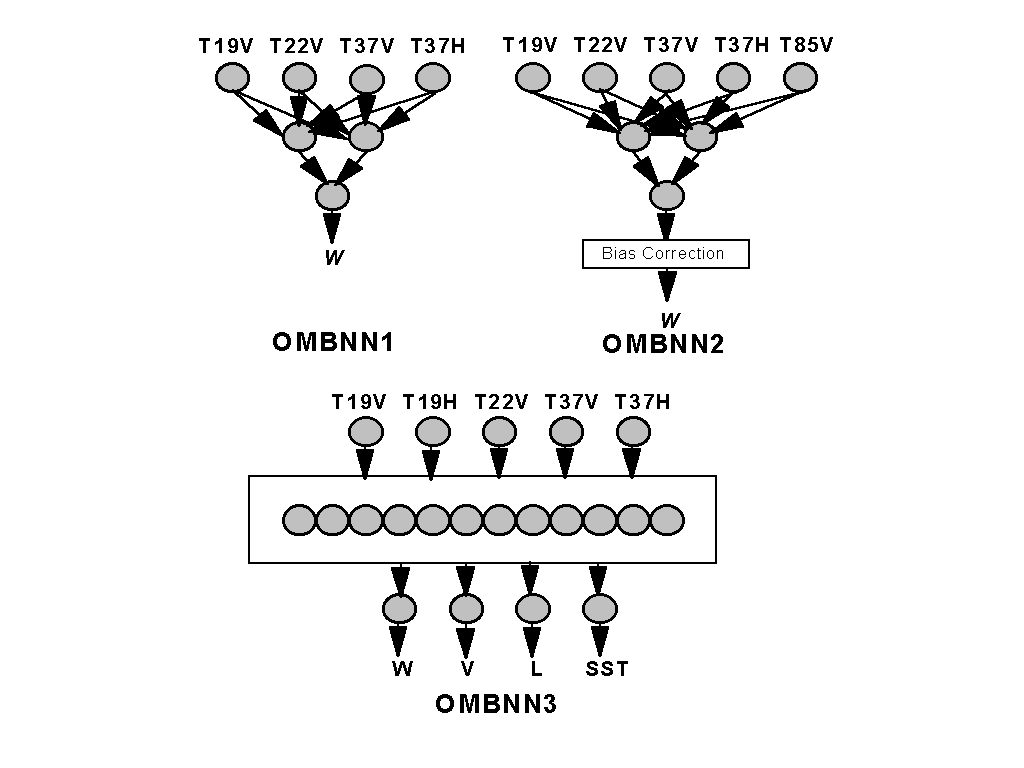
Using the empirical multi-parameter retrieval approach, a new NN architecture was formulated (Fig. 1) which takes into account the interdependence of physically-related atmospheric and oceanic parameters (wind speed, columnar water vapor, columnar liquid water and sea surface temperature) (Krasnopolsky et al. (1996b), Krasnopolsky (1997)). The new OMBNN3 algorithm, described in detail in the next section, utilizes five SSM/I BT channels. Four geophysical parameters are produced simultaneously. This algorithm preserves the correct physical relationships between these parameters. The algorithm not only improves the accuracy of the wind speed retrievals (see Table 2), especially at high wind speeds (without a bias correction) but has also extended the range over which useful wind speed retrievals can be obtained.
Selected properties of the algorithms considered in this study (type, method and SSM/I channels used) are presented in Table 1 below.
Table 1. Properties
of global SSM/I wind speed retrieval algorithms. Abbreviation, mathematical/statistical
method, and channels used are shown. "X " is for the channel utilized in
the algorithm and "x" for the channel utilized in the retrieval flag.
| Algorithm | Method | 19V | 19H | 22V | 37V | 37H | 85V | 85H |
| GSW | Lin. regress. & approx., Single-parameter | X | x | X | X | X | - | - |
| GSWP | Lin. regress., nonlin. approx, Single-parameter | X | x | X | X | X | - | - |
| GS | Nonlin. regress. & approx., Single-parameter | X | X, x | X | X | X | - | - |
| PB | Physically-based, Multi-parameter | X | X | X | X | X | - | - |
| OMBNN1 | Single-parameter NN | X | x | X | X | X | - | - |
| OMBNN2 | Single-parameter NN | X | x | X | X | X | X | - |
| OMBNN3 | Multi-parameter NN | X | X, x | X | X | X | - | - |
Table 2 compares the GSW, GSWP, GS, PB, and OMBNN3 wind speed retrieval algorithms in terms of three separate components of the total RMS error (RMSE). Total RMSE was calculated as the RMS difference between the buoy and the algorithm-derived wind speed. High wind speed RMSE is a part of the total RMSE for events where buoy wind speeds are higher than 15 m/s, indicating the performance of the algorithms at high wind speeds. Algorithm RMSE is the error which is introduced into the retrievals by the algorithm itself, because the algorithm is only an approximation of the true TF. This error was calculated following standard procedures, e.g. (Wentz, 1997, Krasnopolsky, 1997) which remove sensor noise, noise in the buoy observations, and spatial and temporal matching errors, from the total RMSE. Table 2 indicates the importance of accounting for the co-variability of water vapor, liquid water, and SST in the retrieval process for improving the accuracy in retrieving wind speed. The GSWP algorithm improves the total retrieval accuracy compared to the linear GSW algorithm because it includes a water vapor correction which corrects for water vapor "artificial" systematic error. However, it does not significantly improve the performance of the GSW algorithm at high wind speeds because most of the high wind speed events occur at mid- and high-latitudes where the amount of water vapor in the atmosphere is relatively low. In this case, cloud liquid water is the main source of nonlinear behavior in the TF and the source of additional "artificial" errors in the single-parameter retrievals; thus, in this case, the co-variability of liquid water must also be taken into account. The RMS error statistics of the OMBNN3 algorithm, which also take into account the influence of liquid water and SST, are lower than those of the GSWP algorithm over all wind speeds and weather conditions, and especially at wind speeds > 15 m/s.
Table 2. Comparison
of bias, algorithm RMS error (sensor noise and matchup uncertainties removed),
total RMS error and high wind speed (W>15m/s) RMS error, for buoy vs. SSM/I
wind speed, for five SSM/I wind speed algorithms. Errors (in m/s) are calculated
for approximatelly15,000 buoy/SSM/I matchups. Numbers correspond to clear,
and in parentheses, to clear+cloudy conditions.
| Algorithm | Bias | Algorithm RMSE | Total RMSE | W > 15 m/s RMSE |
| GSW | -0.2 (-0.5) | 1.4 (1.8) | 1.8 (2.1) | (2.7) |
| GSWP | -0.1 (-0.3) | 1.3 (1.6) | 1.7 (1.9) | (2.6) |
| GS | 0.5 (0.7) | 1.4 (2.2) | 1.8 (2.5) | (2.7) |
| PB | 0.1 (-0.1) | 1.3 (1.8) | 1.7 (2.1) | (2.6) |
| OMBNN3 | -0.1 (-0.2) | 1.0 (1.3) | 1.5 (1.7) | (2.3) |
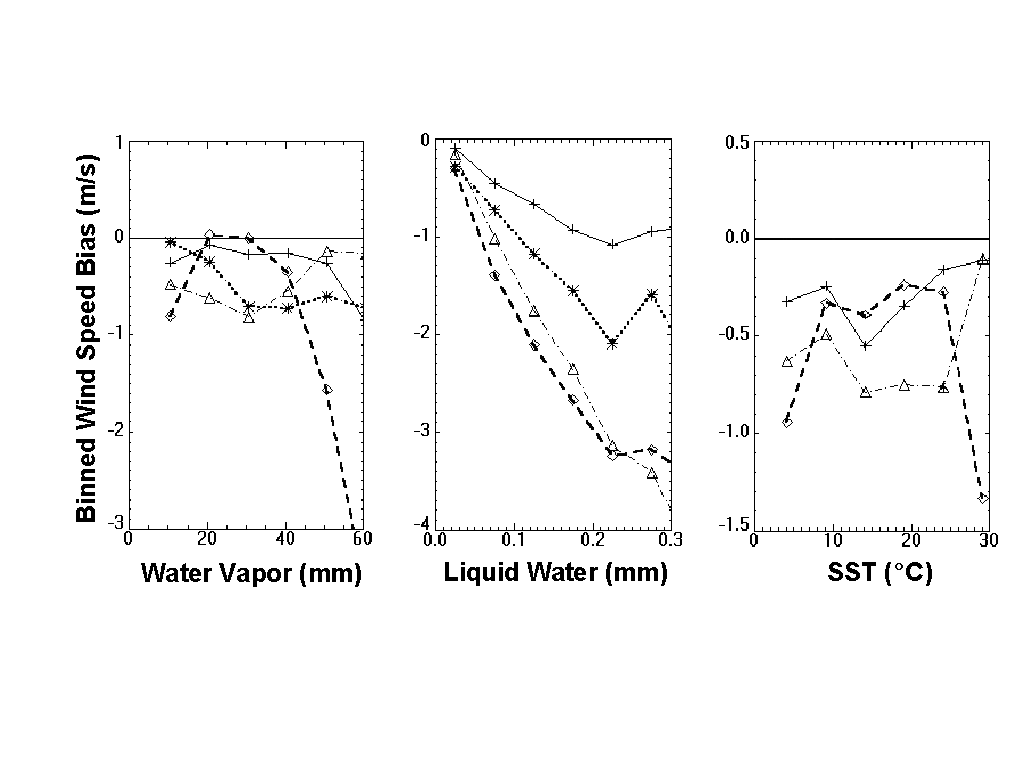
Fig. 2. Binned mean value (bias) of the
difference between the buoy and SSM/I (F10) wind speeds vs. columnar water
vapor, columnar liquid water, and SST. GSW algorithm - dashed line with
diamonds, PB algorithm - dotted line with stars, OMBNN3 - solid line with
crosses, and GSWP algorithm - dash-dotted line with triangles.
Fig. 2 shows the
mean wind speed differences (buoy minus satellite wind speed) or biases
as functions of three other parameters: columnar water vapor, columnar
liquid water, and sea surface temperature for four algorithms, GSW, GSWP,
PB and OMBNN3. Including the nonlinear water vapor correction in GSWP reduces
the bias and its dependence on the water vapor concentration (and partly
on SST which is closely related to water vapor); however, it does not reduce
the dependence on liquid water concentration. The OMBNN3 and PB algorithms,
which both employ the simultaneous multi-parameter retrieval approach,
reduce the bias and dependence of the bias on both water vapor and cloud
liquid water concentration. The PB algorithm does not retrieve SST but
uses SST climatology as required input parameter. Finally, the OMBNN3 algorithm
also demonstrates the best performance with respect to SST co-variability.
A New Multi-Parameter SSM/I Retrieval Algorithm
In this section we introduce a new multi-parameter NN algorithm, OMBNN3. This algorithm contains three innovations. First, the co-variability of related atmospheric and surface parameters which can be extracted from the same set of BTs is taken into account: the entire vector, G = {W, V, L, TS}, of geophysical parameters (here W is wind speed, V is columnar water vapor, L is columnar liquid water, and TS is sea surface temperature (SST)) is retrieved simultaneously as in (13). SST is now an output rather than an additional input as in (7).
Second, a method of NN training which enhances learning at high wind speeds was used (Krasnopolsky et al., 1996a). In preparation for training the NN, the weights, in the error function were generated using the following formula,
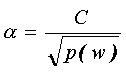
where p(w) is the observed wind speed probability distribution and C is a normalization constant. This choice of weights allows us to assign higher values to the tails of the distribution and to produce a distribution which is approximately uniform. By introducing the square root in the denominator, we have restricted the rate of increase in the weights which reduces noise-like influences at higher wind speeds.
Third, an extensive
new buoy/SSM/I matchup database containing matchup data for the F8, F10,
and F11 sensors(6), augmented with additional
matchup data(7) for high latitudes which
contain a far greater number of high wind speed events (up to 26 m/s),
was used for developing this algorithm. The OMBNN3 algorithm uses five
SSM/I channels: 19 GHz and 37 GHz (horizontal and vertical polarization)
and 22 GHz (vertical polarization). The NN which implements (13) has 5
inputs and 4 outputs, and one hidden layer with 12 nodes (see Fig. 1).
It can be represented by an analytic expression (A5) with n = 5
(inputs), m = 4 (outputs), and k = 12 (hidden nodes). After
the NN is trained (all parameters in (A5) are found), each retrieval of
the vector G is rapidly produced by evaluating expression
(A5) (several tens of floating point additions and multiplications).
The Matchup Database
A raw SSMI/buoy matchup database, originally created by the Navy Research Laboratory, was used as a basis for training and validation. This database contains 3,144 F8/buoy and 12,013 F10/buoy matchups for the period 9/91 to 6/93, and 10,195 F11/buoy matchups for the period 12/91 to 6/93. Both NDBC and TOGA-TAO buoys are included in this matchup database. We have carefully screened the matchups extracted from the NRL database (i.e., applied extensive quality control). More than 30 different criteria have been applied to both the buoy data and the SSM/I BT data to identify missing observations and to remove those which were questionable (see Krasnopolsky et al. (1997) for details). Locations for TOGA-TAO buoys have been corrected using information from the TAO Web Home page. More than 3,000 matchups were removed or corrected. As a second step, we selected matchups for cases where the satellite and buoy data were collocated within 15 km spatially, and 15 minutes, temporally. The additional F11 matchups7 were obtained from the high-latitude European Ocean Weather Stations LIMA (430 matchups) and MIKE (639 matchups). These data were also carefully quality controlled, and the same space/time filter was likewise applied.
For all data and all algorithms considered, wind speeds have been adjusted to a reference height of 20 m. Characteristics of the data selected after quality control and collocation filtering are shown in Table 3. Clear and cloudy conditions are defined below and correspond to the retrieval flags given by Stogryn et al. (1994). These flags account for different weather conditions by separating the BTs into three categories. Clear conditions correspond to clear sky with low levels of columnar liquid water (L < 0.05 mm); cloudy conditions correspond to clouds but no rain with columnar liquid water up to 0.4 - 0.5 mm (Krasnopolsky et al., 1995a). In terms of SSM/I BTs, these conditions are:
T37V - T 37H > 50 K for clear conditions
and
T37V - T 37H 50 K (17)
T19V < T37V
T19H 185 K for cloudy conditions
T37H 210 K
BTs which do not fulfill any of the conditions in (17) correspond to levels of cloud liquid water which are so high that no microwave radiation from the ocean surface reaches the sensor, and thus, no retrievals are possible. We refer to such conditions as "very cloudy" and exclude these matchups from further consideration.
Most of the high wind speeds are correlated with higher levels of moisture and cloudiness (Table 3). Matchup data for F8 and F10 do not contain buoy wind speeds higher than 21.6 m/s even under clear + cloudy conditions. Also, a few of the high wind speed events in these data contain levels of liquid water which are high enough to preclude the possibility of making retrievals. Only the bouy/F11 data contain a significant number of high wind speed events under clear + cloudy conditions (up to 25 m/s).
Table 3. Statistics
for surface in situ wind speed data used for algorithm development and
validation. Columns 2 - 4 show total number of matchups, and the number
of matchups for clear and cloudy conditions separately. Columns 5 - 7 show
statistics for the wind speeds per se (sw
denotes standard deviation) for all matchups, and columns 8 and 9 show
maximum wind speed for clear+cloudy and clear conditions.
| Number of matchups | Mean
W
(m/s) |
sw
(m/s) |
Max
W
(m/s) |
Max
W Clear+Cloudy
(m/s) |
Max
W Clear
(m/s) |
|||
| Total | Clear | Cloudy | ||||||
| Buoy/F08 | 1765 | 1437 | 200 | 7.4 | 3.3 | 26.0 | 21.5 | 18.6 |
| Buoy/F10 | 7495 | 5953 | 926 | 7.3 | 3.2 | 25.0 | 21.6 | 20.5 |
| Buoy/F11 | 6633 | 5274 | 855 | 7.5 | 3.5 | 26.4 | 25.0 | 20.1 |
| LIMA/F11 | 304 | 253 | 51 | 10.4 | 4.9 | 26.4 | 26.4 | 23.9 |
| MIKE/F11 | 243 | 215 | 27 | 9.8 | 4.9 | 24.2 | 24.2 | 21.1 |
As mentioned, to further improve the coverage at high wind speeds, the buoy/F11 data have been supplemented with observations from LIMA/F11 and MIKE/F11. These matchups contain wind speeds up to 26.4 m/s and correspond to high latitudes (LIMA was located at 57N and MIKE at 65N), also improving the geographical distribution of our data (most NDBC buoys are located at mid-latitudes). Both buoy and Ocean Weather Station data include wind speeds and SSTs; however, they do not include columnar water vapor and columnar liquid water. These two parameters were also required for training and validation of the new algorithm. Because we did not have collocated buoy/radiosond/SSMI data for developing this algorithm, we obtained columnar water vapor and columnar liquid water by using cal/val (Alishouse et al., 1990), and Weng and Grody (1994) algorithms. Such single-parameter empirical algorithms, of course, only generate proxies for the "true" data. As shown in the section "Extracting geophysical parameters from satellite data", these single-parameter retrievals may be biased and contain significant random errors which affect NN training and allow only an approximate separation of the V- and L-signals from the other components. However, as Table 2 and Fig. 2 show, even such an approximate separation of signals allows us to reduce the random and systematic errors in wind speed and diminish the dependence of the wind speed bias on V and L.
The resulting blended F11 matchup database has been separated into two independent data sets: one for training and one for testing. In the process of training, the NN was periodically applied to the independent test data. When the bias (mean difference between test and NN-generated data) and RMS error stopped decreasing for the test data, the training process was terminated to prevent overtraining. Usually training and test RMSEs are close at this point. Thus, the statistics for training, testing and training plus test (composite) data are similar. In tables 4 - 6, we present only the composite statistics for F11 (for details, see Krasnopolsky et al., (1996b)). F8 and F10 matchups were not used in the training process. These statistics present an independent validation of OMBNN3.
As shown by Krasnopolsky
et al. (1994, 1995a), NN algorithms can successfully retrieve wind speeds
under clear + cloudy conditions. Therefore, for training, we used all available
buoy/F11 + OWS/F11 matchups which corresponded to clear + cloudy conditions,
according to Stogryn's retrieval flags (17). Statistics for clear conditions
were then calculated by applying the trained NN to the clear portion of
the matchup data. Because higher wind speed events were given extra weight,
noise in this portion of the data could have reduced the effectiveness
of the training process. To minimize this possibility, we additionally
removed a number of outliers at higher wind speeds from the training set,
but no outliers were removed from the test data, or any of the other data
used for validation.
Wind Speed
In this section we
present evaluation statistics for wind speed, the primary output of the
OMBNN3 algorithm, by comparing its performance with all of the previously
mentioned empirical algorithms for the F08, F10, and F11 SSM/I instruments.
The SBB algorithm is not shown because the associated statistics are practically
identical to those for OMBNN1. Retrievals obtained from the physically-based
(PB) algorithm developed by Wentz (1997)(8)
are also included in Tables 4-6. Statistics the other outputs are presented
in the following sections.
Composite wind speed statistics.
Table 4 shows the composite wind speed statistics for clear conditions, and Table 5 shows the statistics for clear + cloudy conditions. Tables 4 and 5 contain statistics for three satellites and seven different algorithms including the mean difference between buoy and SSM/I wind speeds (bias), the standard deviation of the differences (SD), and the correlation coefficient between buoy and SSM/I wind speeds (CC). These tables together with Table 6 also contain buoy wind speed statistics for each data set including maximum wind speed, mean wind speed, and the standard deviation, sw. There are some cases where the empirical algorithms produce satisfactory retrievals whereas the PB algorithm does not converge or it produces negative values for wind speed (even under clear conditions in some cases), a problem which is unique to the PB approach. In Tables 4, 5, and 6, the numbers in parentheses for the PB algorithm show the percent of matchups where this algorithm produced valid retrievals. For example, for the buoy/F10 and buoy/F11 data sets, there are 951 matchups (10% of the total) where the PB algorithm does not converge. The OMBNN3 algorithm produces valid retrievals for these 951 matchups with a bias of 0.3 m/s and an RMS error of 1.9 m/s which are only slightly higher than the values obtained for the entire data set (Table 5). For all algorithms, statistics are calculated for all matchups, with the exception of the PB algorithm where statistics are calculated only for the matchups where it converges.
Summarizing the information
in Tables 4 and 5:
Table 4.
Composite statistics for the GSW, GS, GSWP, PB, OMBNN1, OMBNN2 and OMBNN3
algorithms for clear conditions and for three different SSM/I
instruments. Columns 3 - 5 show statistics for the wind speeds per se (sw
denotes standard deviation), and columns 6 - 8 for the difference between
buoy and algorithm-generated wind speeds. SD denotes standard deviation,
and CC denotes correlation coefficient. N is total number
of matchups.
| Satellite | Max W | Mean W | sw | Bias | SD | CC | |
|
F08
N=1437
|
Buoy | 19.2 | 7.06 | 3.01 | N/A | N/A | N/A |
| GSW | 21.4 | 7.08 | 3.18 | -0.02 | 1.77 | 0.84 | |
| GS | 21.8 | 6.15 | 3.32 | 0.91 | 1.80 | 0.84 | |
| GSWP | 20.7 | 7.01 | 3.18 | 0.05 | 1.60 | 0.86 | |
| PB (92%) | 19.9 | 6.73 | 3.47 | 0.33 | 1.63 | 0.85 | |
| OMBNN1 | 15.1 | 6.13 | 2.38 | 0.93 | 1.49 | 0.87 | |
| OMBNN2 | 16.8 | 6.56 | 2.68 | 0.50 | 1.48 | 0.88 | |
| OMBNN3 | 20.1 | 7.07 | 3.01 | -0.01 | 1.43 | 0.88 | |
|
F10
N=5953 |
Buoy | 20.5 | 6.98 | 2.95 | N/A | N/A | N/A |
| GSW | 20.8 | 7.20 | 3.22 | -0.22 | 1.86 | 0.82 | |
| GS | 21.1 | 6.28 | 3.34 | 0.70 | 1.89 | 0.83 | |
| GSWP | 20.0 | 7.21 | 3.19 | -0.23 | 1.74 | 0.84 | |
| PB (94%) | 19.8 | 6.66 | 3.21 | 0.32 | 1.72 | 0.84 | |
| OMBNN1 | 14.7 | 6.23 | 2.46 | 0.75 | 1.63 | 0.84 | |
| OMBNN2 | 17.1 | 6.13 | 2.61 | 0.84 | 1.60 | 0.84 | |
| OMBNN3 | 20.2 | 7.21 | 2.97 | -0.23 | 1.68 | 0.84 | |
|
F11
N=5742 |
Buoy+OWS | 23.9 | 7.13 | 3.29 | N/A | N/A | N/A |
| GSW | 20.9 | 7.34 | 3.36 | -0.21 | 1.72 | 0.87 | |
| GS | 21.1 | 6.45 | 3.51 | 0.68 | 1.75 | 0.87 | |
| GSWP | 19.6 | 7.30 | 3.36 | -0.16 | 1.62 | 0.88 | |
| PB (89%) | 20.7 | 7.27 | 3.28 | -0.14 | 1.65 | 0.84 | |
| OMBNN1 | 16.9 | 6.47 | 2.55 | 0.66 | 1.55 | 0.89 | |
| OMBNN2 | 17.9 | 6.32 | 2.72 | 0.81 | 1.56 | 0.88 | |
| OMBNN3 | 20.2 | 7.17 | 3.03 | -0.04 | 1.43 | 0.90 |
Table 5. Composite
statistics for the GSW, GS, GSWP, PB, OMBNN1, OMBNN2 and OMBNN3 algorithms
for clear + cloudy conditions and for three different SSM/I
instruments. Columns 3 - 5 show statistics for the wind speeds per se (sw
denotes standard deviation), and columns 6 - 8 for the difference between
buoy and algorithm-generated wind speeds. SD denotes standard deviation,
and CC denotes correlation coefficient. N is total number
of matchups.
| Satellite | Max W | Mean W | sw | Bias | SD | CC | |
|
F08
N=1637 |
Buoy | 21.5 | 7.31 | 3.17 | N/A | N/A | N/A |
| GSW | 25.9 | 7.65 | 3.54 | -0.34 | 2.13 | 0.80 | |
| GS | 35.9 | 6.60 | 3.63 | 0.71 | 2.21 | 0.80 | |
| GSWP | 25.6 | 7.48 | 3.50 | -0.17 | 1.88 | 0.84 | |
| PB (92%) | 25.5 | 6.98 | 3.84 | 0.35 | 2.12 | 0.82 | |
| OMBNN1 | 17.1 | 6.32 | 2.45 | 0.99 | 1.62 | 0.86 | |
| OMBNN2 | 18.4 | 6.80 | 2.92 | 0.51 | 1.60 | 0.87 | |
| OMBNN3 | 20.6 | 7.41 | 3.09 | -0.10 | 1.59 | 0.87 | |
|
F10
N=6879 |
Buoy | 21.6 | 7.26 | 3.18 | N/A | N/A | N/A |
| GSW | 26.0 | 7.81 | 3.59 | -0.55 | 2.15 | 0.80 | |
| GS | 52.9 | 6.72 | 3.70 | 0.54 | 2.29 | 0.79 | |
| GSWP | 26.8 | 7.68 | 3.51 | -0.42 | 1.94 | 0.84 | |
| PB (99%) | 31.1 | 7.15 | 3.66 | 0.11 | 2.13 | 0.81 | |
| OMBNN1 | 16.4 | 6.42 | 2.53 | 0.85 | 1.74 | 0.84 | |
| OMBNN2 | 19.5 | 6.32 | 2.77 | 0.95 | 1.72 | 0.84 | |
| OMBNN3 | 22.5 | 7.57 | 3.18 | -0.31 | 1.79 | 0.84 | |
|
F11
N=6675 |
Buoy+OWS | 26.4 | 7.47 | 3.51 | N/A | N/A | N/A |
| GSW | 30.3 | 7.99 | 3.77 | -0.53 | 2.09 | 0.84 | |
| GS | 618.9 | 7.06 | 8.87 | 0.41 | 8.19 | 0.39 | |
| GSWP | 31.2 | 7.83 | 3.74 | -0.36 | 1.92 | 0.86 | |
| PB (91%) | 35.4 | 7.84 | 3.73 | -0.36 | 2.10 | 0.85 | |
| OMBNN1 | 19.4 | 6.70 | 2.65 | 0.76 | 1.70 | 0.88 | |
| OMBNN2 | 20.7 | 6.56 | 2.90 | 0.91 | 1.70 | 0.88 | |
| OMBNN3 | 22.8 | 7.57 | 3.27 | -0.11 | 1.61 | 0.89 |
Table 2 shows a summary comparison of the GSW, GSWP, PB, and OMBNN3 algorithms using all available matchups for F8, F10, and F11. An error analysis (Wentz, 1997; Krasnopolsky, 1997) was performed where sensor and observation errors were estimated separately and removed (for simplicity we assume that observation and sensor errors in wind speed do not depend on the retrieval algorithm). The algorithm errors themselves were then extracted. After removing the sensor and observation errors, the improved performance of the OMBNN3 algorithm (RMS errors of 1 m/s for clear-, and 1.3 m/s for clear+cloudy conditions) becomes even more apparent.
As mentioned above,
one of the advantages of the OMBNN3 algorithm is its ability to retrieve
not only wind speed but also three other parameters: columnar water vapor
V,
columnar liquid water L, and SST. The accuracies of these
additional retrievals are discussed below. Fig.
2 demonstrates how simultaneous
retrievals of the entire vector of related geophysical parameters (13)
improves the accuracy of the wind speed retrievals by taking into account
the co-variability of the related parameters. Figs. 2 shows the systematic
errors in wind speed retrieval (bias) as functions of V,L, and SST
for the GSW, GSWP, PB, and OMBNN3 algorithms. The errors for the OMBNN3
algorithm show the weakest dependencies on the related atmospheric and
surface (SST) parameters as compared with the errors for the other
algorithms.
High wind speed statistics.
Table 6 shows statistics calculated separately for wind speeds > 15 m/s.
Although the sample sizes are small in each case, certain conclusions can be drawn from the table. At high wind speeds, the OMBNN3 algorithm performs significantly better than the other algorithms, based on the SD. All algorithms, except for the NN-based algorithms, show a tendency to overestimate high wind speeds. This happens because high wind speed events are usually accompanied by a significant amount of cloud liquid water. Under such circumstances,
Table 6.
High winds (W > 15 m/s) statistics for algorithms presented in Table 2,
for clear+cloudy conditions and for three different SSM/I
instruments. Columns 3 - 5 show statistics for the wind speeds per se (sw
denotes standard deviation), and columns 6 - 7 for the difference between
buoy and algorithm-generated wind speeds. SD denotes standard deviation.
N
is total number of matchups.
| Satellite | Max W | Mean W | sw | Bias | SD | |
|
F08
N=33
|
Buoy | 21.5 | 16.8 | 1.55 | N/A | N/A |
| GSW | 21.4 | 16.9 | 2.97 | -0.10 | 1.52 | |
| GS | 21.8 | 16.3 | 2.65 | 0.44 | 2.30 | |
| GSWP | 20.7 | 16.5 | 1.83 | 0.25 | 1.52 | |
| PB (88%) | 19.9 | 16.1 | 2.02 | 0.72 | 1.76 | |
| OMBNN3 | 20.6 | 16.4 | 1.76 | 0.42 | 1.40 | |
|
F10
N=155 |
Buoy | 21.6 | 16.8 | 1.51 | N/A | N/A |
| GSW | 26.0 | 17.1 | 2.95 | -0.3 | 2.61 | |
| GS | 27.7 | 16.3 | 4.12 | 0.53 | 3.88 | |
| GSWP | 26.8 | 16.9 | 2.94 | -0.05 | 2.61 | |
| PB (89%) | 31.1 | 16.2 | 3.31 | 0.60 | 2.88 | |
| OMBNN3 | 22.5 | 16.4 | 2.62 | 0.40 | 2.16 | |
|
F11
N=212 |
Buoy+OWS | 26.4 | 17.5 | 2.34 | N/A | N/A |
| GSW | 30.3 | 17.0 | 2.98 | 0.46 | 2.68 | |
| GS | 117.5 | 17.2 | 8.69 | 0.35 | 8.38 | |
| GSWP | 31.2 | 16.8 | 3.02 | 0.70 | 2.68 | |
| PB (54%) | 35.4 | 16.6 | 3.50 | 0.91 | 3.09 | |
| OMBNN3 | 22.8 | 16.3 | 2.50 | 1.17 | 2.25 |
the TF becomes a
complicated nonlinear function, and simple, single-parameter regression-based
algorithms can not adequately represent this function, and often, high
concentrations of cloud liquid water are confused with high wind speeds.
OMBNN3, because it is nonlinear and accounts for the co-variability of
cloud liquid water and SST, produces smaller errors at high wind speeds.
For wind speeds > 22 m/s, where the noise level is also highest (see discussion
in Krasnopolsky et al. (1996a)), OMBNN3 has retrieval errors of about 10
- 15% and slightly underestimates high wind speeds by about 10%.
Other Parameters.
OMBNN3 has also been trained to retrieve columnar water vapor, V, columnar liquid water, L, and SST, using the same SSM/I TBs. Values of V generated by the cal/val algorithm of Alishouse et al. (1990), values of L from the algorithm of Weng and Grody (1994) (WG), and buoy measurements of SST were used as ground truth (SST) or in the case of V and L as proxies for ground truth during the training. As explained in the previous section, we used proxies for V and L because the appropriate ground truth data (buoy/radiosonde/SSMI) matchups were not available. Table 7 shows retrieval statistics for columnar water vapor (maximum V, mean V, and standard deviation sV) for the cal/val, PB, Petty (1993) and OMBNN3 algorithms. It also shows the bias, SD of the differences between the cal/val and PB, Petty, and OMBNN3, and the correlation coefficient (CC) between cal/val, PB, Petty and OMBNN3 retrievals. The OMBNN3 and Petty algorithms reproduce the cal/val retrievals closely with a SD of about 1 mm, and for the PB retrievals, the SD is about 2 mm. Also, for the PB algorithm, the mean difference (bias) is larger.
Table 7. Statistics
for columnar water vapor V (mm) retrieved by cal/val, PB, Petty,
and OMBNN3 algorithms for clear + cloudy conditions and for
F10 and F11 SSM/I instruments. Columns 3 - 5 show statistics for the columnar
water vapor per se (sV
denotes standard deviation), and columns 6 - 8 for the difference between
cal/val and Petty, or PB, or OMBNN3 algorithm-generated columnar water
vapor. SD denotes standard deviation, and CC denotes correlation coefficient.
N
is total number of matchups.
| Satellite | Algorithm | Max V | Mean V | sV | Bias | SD | CC |
|
F10 N=6879 |
Alishouse | 60.8 | 31.0 | 14.7 | N/A | N/A | N/A |
| Petty | 64.7 | 31.2 | 15.1 | -0.2 | 1.1 | 1.0 | |
| PB (96%) | 69.7 | 30.4 | 14.6 | 0.6 | 1.6 | 0.97 | |
| OMBNN3 | 59.2 | 30.9 | 15.4 | 0.1 | 1.1 | 1.0 | |
|
F11 N=6675 |
Alishouse | 64.4 | 31.6 | 15.2 | N/A | N/A | N/A |
| Petty | 69.2 | 31.6 | 15.2 | 0.0 | 1.2 | 1.0 | |
| PB (91%) | 73.1 | 30.9 | 15.4 | 0.7 | 1.8 | 0.97 | |
| OMBNN3 | 60.1 | 31.4 | 15.7 | 0.3 | 0.9 | 1.0 |
Table 8. Statistics
for columnar liquid water L (mm) retrieved by WG and OMBNN3 algorithms
for clear + cloudy conditions and for F10 and F11 SSM/I instruments.
Columns 3 - 5 show statistics for the columnar liquid water per se (sL
denotes standard deviation), and columns 6 - 8 for the difference between
WG and OMBNN3 algorithm-generated columnar liquid water. SD denotes standard
deviation, and CC denotes correlation coefficient. N is total
number of matchups.
| Satellite | Algorithm | Max L | Mean L | sL | Bias | SD | CC |
| F10
N=6879 |
Weng, Grody | 0.44 | 0.034 | 0.058 | N/A | N/A | N/A |
| OMBNN3 | 0.38 | 0.039 | 0.058 | 0.005 | 0.016 | 0.96 | |
| F11
N=6675 |
Weng, Grody | 0.38 | 0.034 | 0.058 | N/A | N/A | N/A |
| OMBNN3 | 0.36 | 0.036 | 0.057 | 0.00 | 0.015 | 0.97 |
Table 8 shows retrieval statistics for columnar liquid water (maximum L, mean L, and standard deviation sL) for the WG and OMBNN3 algorithms. Again, it shows the mean difference, SD of the difference between WG and OMBNN3, and CC between WG and OMBNN3 retrievals.
Finally, Table 9
shows retrieval statistics for SST (maximum, mean, and standard
deviation, sSST)
based on the OMBNN3 algorithm. The bias, SD, and CC for OMBNN3 vs. the
buoy observations are included. OMBNN3 reproduces the in situ SSTs
with an RMS error of < 5 C, and a bias < 0.7C. Obtaining higher accuracies
for SST from microwave measurements which do not include the frequency
band around 6.6 GHz (Milman and Wilheit, 1985) is probably not achievable.
Although these retrievals have low spatial resolution (of order of SSM/I
footprint size), they can be made in the presence of light and moderate
cloud cover (not under very cloudy conditions as specified in (17)). Most
importantly, however, by incorporating SST as an additional output,
we have avoided the problem of specifying SST as an external parameter,
and have, at the same time, improved the accuracy of the wind speed retrievals
at higher wind speeds.
Table 9. Statistics
for SST (C) retrieved by OMBNN3 vs. buoy for CLEAR + CLOUDY conditions
for F10 and F11 SSM/I instruments. Columns 3 - 5 show statistics for the
SST (sSST
denotes standard deviation), and columns 6 - 8 for the difference between
buoy and OMBNN3-generated SST. SD denotes standard deviation, and CC denotes
correlation coefficient. N is total number of matchups.
| Satellite | Source | Max SST | Mean SST | sSST | Bias | SD | CC |
| F10
N=6847 |
Buoy | 31.0 | 20.7 | 8.57 | N/A | N/A | N/A |
| OMBNN3 | 31.0 | 20.16 | 8.29 | 0.58 | 4.87 | 0.83 | |
| F11
N=5673 |
Buoy | 31.3 | 20.0 | 8.86 | N/A | N/A | N/A |
| OMBNN3 | 30.7 | 20.7 | 7.91 | -0.68 | 4.52 | 0.86 |
Multi-parameter SSM/I Retrievals.
OMBNN3 has been carefully tested(9) using operational data from F10, F11, F13 and F14 SSM/I instruments since mid-1997. The wind speed, columnar water vapor and columnar liquid water fields retrieved by OMBNN3 can be seen on our web site at: http://polar.ncep.noaa.gov/marine.meteorology/marine.winds. Comparisons of the various fields from OMBNN3 reveal important information concerning significant weather over the ocean:
(1) The new algorithm generates high wind speeds (> 20 m/s) in areas where high wind speed events are supported by both subjective and objective analyses.
(2) The NN algorithm clearly separates the wind speed, columnar water vapor, and columnar liquid water signals contained in the SSM/I BTs. Multi-parameter retrievals preserve the correct physical relationships between the retrieved parameters. For example, there is a clear correlation between areas with higher amounts of cloud liquid water and higher wind speeds , but they are not identical. The areas with the highest wind speeds usually do not correspond precisely to the areas with the highest amounts of liquid water and vice versa. Higher amounts of columnar liquid water are related to areas of water vapor convergence which are closely associated with active frontal locations. These fronts and cyclonic patterns can be seen in both the SSM/I wind speed and columnar liquid water fields, consistent with independent analyses.
(3) On the other hand, the structure of the water vapor field is very different from the fields for wind speed and liquid water; high values of water vapor are related to a moist atmosphere which usually originates from subtropical sources.
(4) SST reveals the expected gradual increase in temperature proceeding from high latitudes to low latitudes in general agreement with climatological SSTs.
Fig. 3 shows composite wind speed (a), columnar liquid water (b), and columnar water vapor (c) retrievals using the OMBNN3 algorithm for the F11, F13, and F14 SSM/I instruments. It also shows buoy and ship wind reports (d), wind vectors from the ERS-2 scatterometer (e), and an objective analysis for surface pressure (f). The marine weather analysis for the northwestern Atlantic on 10 March 1998, at 00UTC shows a major storm system moving across New York, with a cold front (trough) moving eastward across coastal and offshore waters from New York to Florida. There are two storm systems in the Atlantic, one to the north near 37 N and 56 W with a central pressure of 1010 mb, and the other to the south near 26 N and 59 W with a central pressure of 1009 mb. Between these systems is a center of high pressure near 49 N and 58 W with a central pressure of 1039 mb, oriented from southwest to northeast across the region.
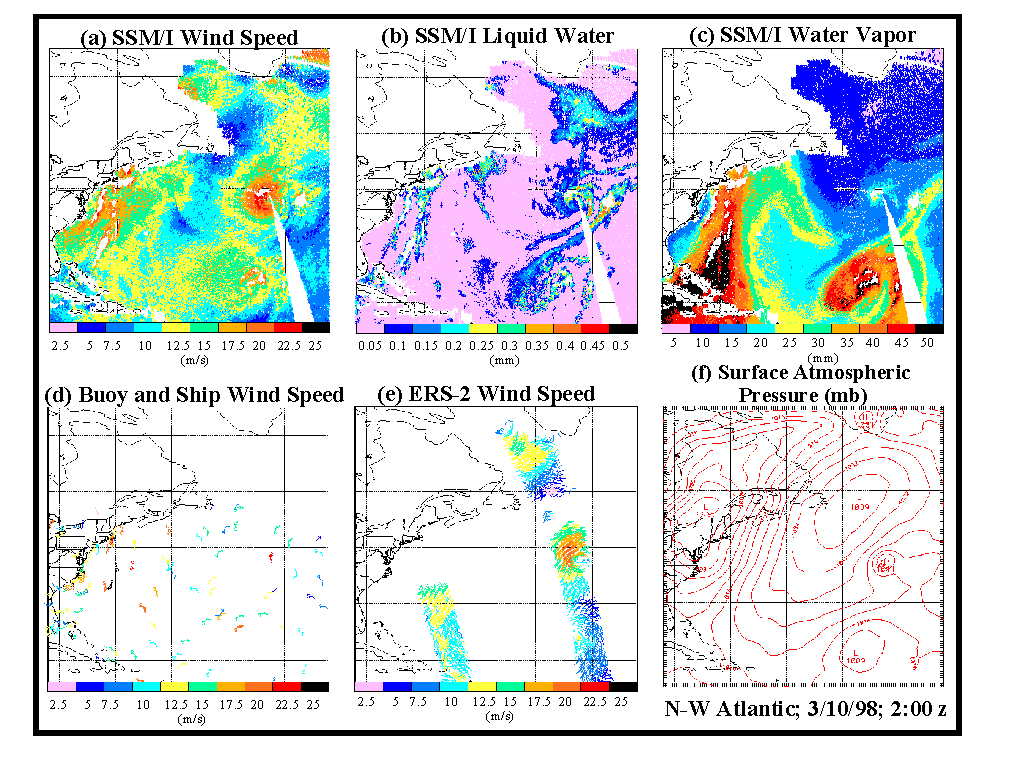
The SSM/I wind pattern (Fig. 3a) and the surface pressure analysis (Fig. 3f) are in agreement, both showing moderate wind speeds ( 35 knots(10)) in advance of the cold front (trough) off the U.S. east coast. Water vapor (Fig. 3c) depicts the location of the front off the east coast, as a zone of strong water vapor gradient where V changes from high values of 45 mm in the warm air before the front to low values of 15-20 mm in the following cold air. Liquid water (Fig. 3b) shows two distinct bands off the east coast, each probably associated with rain showers. The western-most band is aligned with the water vapor gradient zone, in the warm air along the leading edge of the cold front.
Further out in the Atlantic, the system to the north has a tight pressure gradient which agrees with the large area of SSM/I winds with speeds of up to 40 knots; the system to the south has a weaker pressure gradient with only a small area of SSM/I winds with speeds up to 35 knots. The southern system contains high values of water vapor (50 mm) whereas the northern system shows much lower values of water vapor (20-25 mm), consistent with our expectations. The liquid water and water vapor patterns suggest that there is a front lying along the northern boundary of the water vapor gradient maximum, indicating that the northern low lies in the cold air, whereas the southern low is tropical in nature just south of the front. A swath of coincident wind vectors from the ERS-2 scatterometer (Fig. 3e) indicates wind speeds of up to 40 knots around the northern system, in good agreement with the SSM/I wind speeds (Fig. 3a). The final plot (Fig. 3d) of surface observations (ships and buoys) shows that the weather pattern inferred from these various sources of data generally agrees with the SSM/I data.
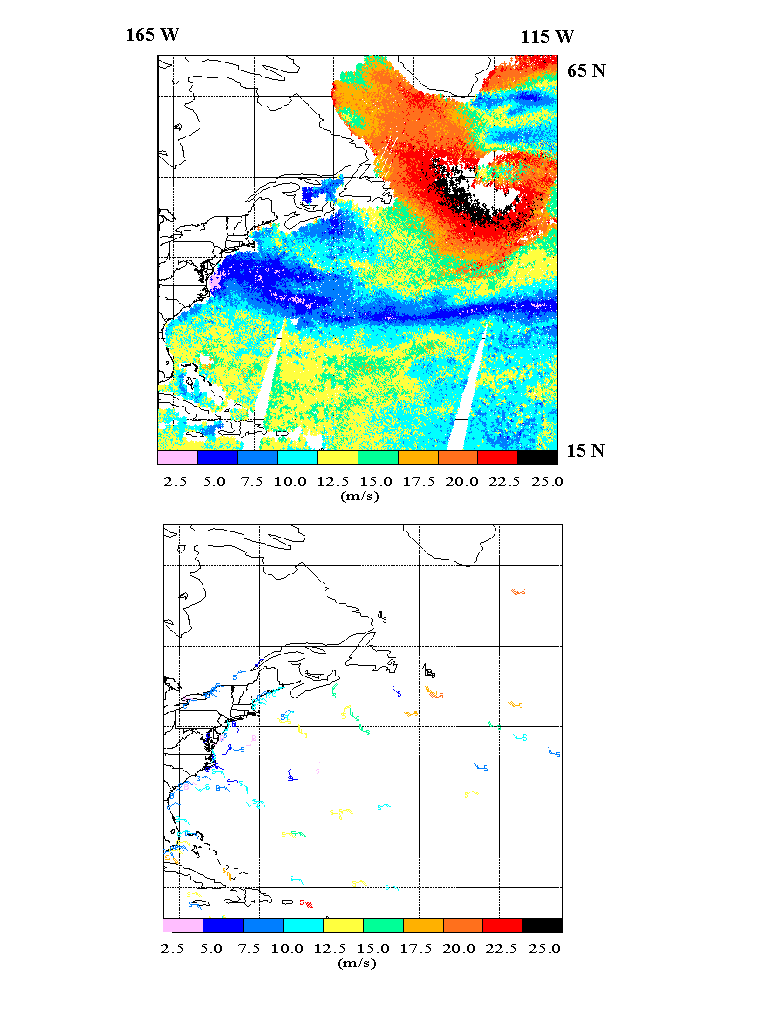
Fig. 4 shows another cyclone in the northwest Atlantic on January 5, 1997. Values of SSM/I wind speed (upper panel) reach up to 25 m/s (in black). Ships and buoys (lower panel) in the same area also reported wind speeds of up to 25 m/s.
Conclusions
We have developed a new empirical, multi-parameter SSM/I retrieval algorithm based on the neural network approach (OMBNN3). This algorithm simultaneously retrieves wind speed, columnar water vapor, columnar liquid water, and SST using only SSM/I BTs. The accuracy of the wind speed retrievals from the new OMBNN3 algorithm (algorithm RMS error of 1.0 m/s under clear, and 1.3 m/s under clear plus cloudy conditions) is systematically higher than the accuracy of the wind speed retrievals from all other algorithms developed to date. This improvement includes all weather conditions where retrievals are possible, and particularly at high wind speeds.
The new algorithm successfully separates wind speed, columnar water vapor, columnar liquid water, and SST information contained in the SSM/I BTs. Multi-parameter retrievals preserve the correct physical relationships between the retrieved parameters. In terms of wind speed, this approach reduces both systematic and random "artificial" errors which are unavoidable using the single-parameter retrieval approach. The OMBNN3 algorithm also reproduces the results of the single-parameter algorithms which have been used to simulate the training data for columnar water vapor and columnar liquid water; however, some interesting differences also arise (e.g., columnar water vapor at high concentrations) which may be due to the fact that this algorithm takes into account interdependencies between the parameters which are retrieved simultaneously. This topic deserves further attention.
Although the SST retrievals are less accurate and have lower spatial resolution, they can be estimated in the presence of cloud. Incorporation of SST as an additional output from the NN allows us to take into account the co-variability of SST without specifying SST as an additional input from an external source. It also improves the accuracy of the wind speed retrievals, especially at high wind speeds.
The simultaneous retrieval of related atmospheric and surface parameters is also beneficial when cloudy and very cloudy weather conditions are present. Because the BT retrieval flags which we use are essentially statistical (based on global statistics), they are not highly sensitive to local conditions. In some cases this may lead to degraded retrievals; therefore, any additional information about related local atmospheric and surface conditions which can be derived from the same BTs may help to improve these BT retrieval flags. Local atmospheric and surface parameters (V, L, and SST), which the OMBNN3 algorithm now produces simultaneously with wind speed, may also help to further improve the accuracy of retrievals under cloudy conditions.
Improvements in the accuracy of wind speed retrievals achieved with OMBNN3 are due to a combination of three factors (see previous section entitled "A new multi-parameter SSM/I retrieval algorithm"), a new multi-parameter retrieval approach, a new method of NN training, and a new, more comprehensive, matchup database. Here, we have concentrated on algorithm description and documenting the overall improvement in retrieval accuracy. Future work will address in more detail the issue of quantifying improvements in the accuracy of retrieving wind speed due to each factor, separately.
In the case of multi-parameter retrievals, the multi-parameter matchup database which is required for algorithm development must be more comprehensive than the single-parameter matchup database used in the single-parameter case, because it contains several geophysical parameters matched with the SSM/I BTs. However, this additional information about related parameters (V, L, and SST) is required only for the training of additional outputs and thus must be included only in the data used for algorithm development. Thus, after training is complete, the multi-parameter algorithm uses only SSM/I BTs and does not require any additional information to produce retrievals for W, V, L, and SST. In our study, proxies for actual observations have been used to provide estimates of V and L in our multi-parameter matchup database. As soon as a database containing buoy/radiosonde/SSMI matchups is available, we will retrain our algorithm using actual ground truth data to further reduce the "artificial" errors, and thus improve the accuracy of retrieving wind speed and the other parameters.
In this study, we have introduced a new generic approach for developing multi-parameter empirical retrieval algorithms based on the NN technique. This approach may find application in other areas of remote sensing as well.
We take this opportunity to thank D.B.
Rao for a thorough review of this manuscript. We also thank the Naval Research
Laboratory for providing us with the new database containing the raw buoy/SSM/I
matchups, David Kilham of Bristol University for providing us with additional
matchup data for high latitudes, and Michael McPhaden and Linda Magnum
for providing us with additional information concerning the TOGA-TAO buoys.
APPENDIX A
A Review of Mathematical Tools Used for Developing Empirical Retrieval Algorithms
The generic empirical retrieval problem (8) is essentially a mapping which maps a vector of sensor measurements, X (T for SSM/I) in Rn, to a vector of geophysical parameters Y (G for SSM/I) in Rm. For empirical retrievals, this mapping is constructed using discrete sets of collocated vectors X and Y or matchup data sets {Xp , Yp}. Single-parameter algorithms (9) may be considered as degenerate mappings where a vector is mapped onto a scalar (or a vector space onto a line). This empirical mapping can be performed using conventional tools (linear and nonlinear regression) and NNs.
Linear regression is an appropriate tool for developing many empirical algorithms. It is simple to apply and has a well-developed theoretical basis. In the case of linear regression, a linear model is constructed for fmod, (8),
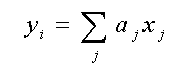
e.g., (14). This model is linear with respect to both a and X , thus it provides a linear approximation of the TF with respect to X. The most important limitation of such a linear approximation is that it works well over a broad range of variability of the arguments only if the function which it represents (TF in our case) is linear. If the TF, f, is nonlinear, linear regression can only provide a local approximation; when applied globally, the approximation becomes inaccurate.
Because, TFs are generally nonlinear functions of their arguments X, linear regression and a nonlinear approximation with respect to X is often better suited for modeling TFs. In this case, fmod can be introduced as a linear expansion using a basis of nonlinear functions {jj }:
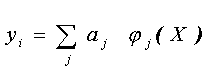 (A1)
(A1)
e.g. (16). Finally, nonlinear regression may be applied. For example, fmod in (8) can be specified as a complicated nonlinear function, fNR:
yi = fNR (X, a ) (A2)
e.g. (15). The expression (A1) is nonlinear with respect to its argument X but linear with respect to the parameters a. The nonlinear regression (A2) is nonlinear both with respect to its argument, X, and with respect to the vector of regression coefficients, a. However, in either case, we must specify in advance a particular type of nonlinear function fNR, or jj. Thus, we are forced to implement a particular type of nonlinearity a priori. This may not always be possible, because we may not know in advance what kind of nonlinear behavior a particular TF demonstrates, or this nonlinear behavior may be different in different regions of the TF's domain. If an inappropriate nonlinear regression function is chosen, it may represent a nonlinear TF with less accurcy than with its linear counterpart, e.g. (15).
In the situation described above, where the TF is nonlinear and the form of nonlinearity is not known, we need a more flexible, self-adjusting approach that can accommodate various types of nonlinear behavior representing a broad class of nonlinear mappings. Neural networks (NNs) are well-suited for a very broad class of nonlinear approximations and mappings. Neural networks consist of layers of uniform processing elements, nodes, units, or neurons. The neurons and layers are connected according to a specific architecture or topology. Fig. A1 shows a simple architecture which is sufficient for any continuous nonlinear mapping, a multilayer perceptron. The number of input neurons, n, in the input layer is equal to the dimension of input vector X. The number of output neurons, m, in the output layer is equal to the dimension of the output vector Y. A multilayer perceptron always has at least one hidden layer with k neurons.
A typical neuron (processing element) usually has several inputs (components of vector X), one output, zj, and consists of two parts, a linear part and a nonlinear part. The linear part forms the inner product of the input vector X with a weight vector Wj (which is one column of the weight matrix Wji ), and a bias term, Bj, may also be added. This linear transformation of the input vector X feeds into the nonlinear part of the neuron as the argument of an activation function. For the activation function, it is sufficient that it be a Tauber-Wiener (nonpolynomial, continuous, bounded) function (Chen and Chen, 1995). Here we use a standard activation function - the hyperbolic tangent. Then, the neuron output, zj , can be written as,
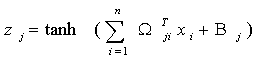
![]() (A3)
(A3)
The neuron is a nonlinear element because its output zj is a nonlinear function of its inputs X.
From the discussion above it is clear that
a NN generally performs a nonlinear mapping of an input vector X
in Rn (n is the dimension of the input
vector or the number of inputs) onto an output vector Y in
R m (m is the dimension of the output vector
or the number of outputs). Symbolically, this mapping can be written as,
Y = fNN(X )
(A4)
where fNN denotes this neural network mapping (the NN input/output relation).
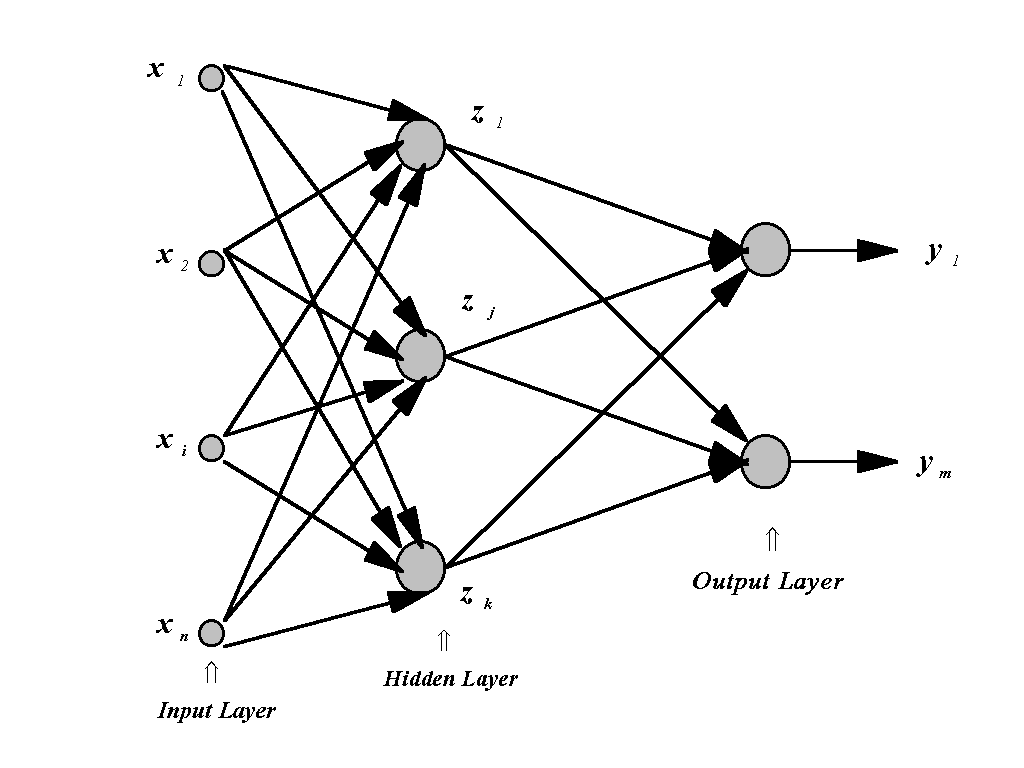
For the topology shown in Fig. A1 for a NN with k neurons in one hidden layer, and using (A3) for each neuron in the hidden and output layers, (A4) can be written explicitly as,
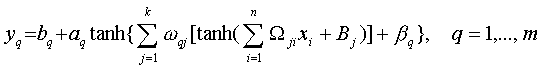 (A5)
(A5)
where the matrix Wji and the vector Bj represent weights and biases in the neurons of the hidden layer; wqj in Rk×m and the bq in Rm represent weights and biases in the neurons of the output layer; and aq and bq are scaling parameters. It can be seen from (A5) that any component (yq) of the NN's output vector Y is a complicated nonlinear function of all components of the NN's input vector X. It has been shown (e.g., Chen and Chen, 1995; Hornik, 1991; Funahashi, 1989; Gybenko, 1989) that a NN with one hidden layer (e.g., NN (A5)), can approximate any continuous mapping defined on compact sets in Rn.
Thus, any problem which can be mathematically reduced to a nonlinear mapping as in (2), (8), or (13) can be solved using the NN represented by (A5). NNs are robust with respect to random noise and sensitive to systematic, regular signals (e.g., Kerlirzin and Réfrégier, 1995). NN solutions given by (A5) for different problems will differ in several important ways. For each particular problem, n and m are determined by the dimensions of the input and output vectors X and Y. The number of hidden neurons, k, in each particular case should be determined taking into account the complexity of the problem. The more complicated the mapping, the more hidden neurons that are required. Unfortunately, there is no universal rule that applies. Usually k is determined by experience and experiment. In general, if k is too large, the NN will reproduce noise as well as the desired signal. Conversely, if k is too small, the NN is unable to reproduce the desired signal accurately. After these topological parameters are defined, the weights and biases can be found, using a procedure called NN training. A number of methods have been developed for NN training (e.g.,Beale and Jackson, 1990; Chen, 1996). Here we use a simplified version of the steepest (or gradient) descent method known as the back-propagation training algorithm. Although NN training is often time consuming, NN application, after training, is not. After the training is finished (it is usually performed only once), each application of the trained NN is practically instantaneous and yields an estimate for (A5) with known weights and biases.
Because the dimension of the output vector Y may obviously be greater than one, NNs are well suited for modeling multi-parameter TFs (13). All components of the output vector Y are produced from the same input vector X. They are related through common hidden neurons; however, each particular component of the output vector Y is produced by a separate output neuron which is unique.
REFERENCES
Alishouse, J.C., et al., 1990, "Determination of Oceanic Total Precipitable Water from the SSM/I. IEEE Trans. Geosci. Remote Sens., GE 23, pp. 811-816
Beale, R. and T. Jackson, 1990, Neural Computing: An Introduction, Adam Hilger, Bristol, Philadelphia and New York
Chen, C.H. (Editor in Chief), 1996, Fuzzy Logic and Neural Network Handbook, McGraw-Hill, New York
Chen, T., and H. Chen, 1995, "Approximation
Capability to Functions of Several Variables, Nonlinear Functionals and
Operators by Radial Basis Function Neural Networks,"
Neural Networks,
Vol. 6, pp. 904-910,
- "Universal Approximation to Nonlinear
Operators by Neural Networks with Arbitrary Activation Function and Its
Application to Dynamical Systems", Neural Networks, Vol. 6, pp.
911-917
Funahashi, K., 1989, "On the Approximate Realization of Continuous Mappings by Neural Networks," Neural Networks, Vol. 2, pp. 183-192
Goodberlet,M.A., C.T.Swift and J.C.Wilkerson, 1989, "Remote Sensing of Ocean Surface Winds With the Special Sensor Microwave Imager. JGR, Vol. 94, pp. 14574 - 14555.
Goodberlet M.A. and C.T. Swift, 1992, "Improved Retrievals from the DMSP Wind Speed Algorithm Under Adverse Weather Conditions, IEEE Trans. Geosci. Remote Sens., 30, pp. 1076-1077.
Gybenko, G., 1989, "Approximation by Superposition of Sigmoidal Functions," in Mathematics of Control, Signals and Systems, Vol. 2, No. 4, pp. 303-314
Hollinger, J., R. Lo, G. Poe, R. Savage, and J. Pierce, 1987, "Special Sensor Microwave/Imager User's Guide", Technical Report, 120 pp, Nav. Res. Lab., Washington, D.C.
Hornik, K., 1991, "Approximation Capabilities of Multilayer Feedforward Network", Neural Networks, Vol. 4, pp. 251-257
Kerlirzin, P., P. Réfrégier, 1995, " Theoretical Investigation of the Robustness of Multilayer Perceptrons: Analysis of the Linear Case and Extension to Nonlinear Networks", IEEE Transactions on neurl networks, Vol. 6, pp. 560-571
Krasnopolsky V.M., L.C. Breaker, and W.H. Gemmill, 1994, "Development of a Single "All-Weather" Neural Network for Estimating Ocean Surface Winds from the Special Sensor Microwave Imager." Technical Note, OPC contribution No. 94, NMC/NOAA
Krasnopolsky, V., L.C. Breaker, and W.H. Gemmill, 1995a, "A neural Network as a Nonlinear Transfer Function Model for Retrieving Surface Wind Speeds from the Special Sensor Microwave Imager", J. Geophys. Res, 100:11,033-11,045
Krasnopolsky, V., W.H. Gemmill, and L.C. Breaker, 1995b, "Improved SSM/I Wind Speed Retrievals at High Wind Speeds. Technical Note, OMB contribution No. 111, NCEP/NOAA
Krasnopolsky V., W.H. Gemmill, L.C. Breaker, and V. Yu. Raizer, 1996a, "An SSM/I Wind Speed Retrieval Algorithm with Improved Performance at Higher Wind Speeds. Technical Note, OMB contribution No. 132, NCEP/NOAA
Krasnopolsky, V., W.H. Gemmill, and L.C. Breaker, 1996b, "A New Transfer Function for SSM/I Based on an Expanded Neural Network Architecture". Technical Note, OMB contribution No. 137, NCEP/NOAA
Krasnopolsky, V., 1997, "Neural Networks for Standard and Variational Satellite Retrievals", Technical Note, OMB contribution No. 148, NCEP/NOAA
Milman, A.S. and T.T. Wilheit, 1985, "Sea Surface Temperature from the Scanning Multichannel Microwave Radiometer on Nimbus-7", J. Geophys. Res, Vol. 90, pp. 11631-41
Petty, G.W., 1993, "A comparison of SSM/I Algorithms for the Estimation of Surface Wind", Proceedings Shared Processing Network DMSP SSM/I Algorithm Symposium, 8-10 June 1993
Stogryn A.P., C.T. Butler, and T.J. Bartolac, 1994, "Ocean Surface Wind Retrievals from Special Sensor Microwave Imager Data with Neural Networks", J. Geophys. Res., Vol. 90, pp. 981-984
Thiria, S., C. Mejia, F. Badran, and M. Crepon, 1993 , "A Neural Network Approach for Modeling Nonlinear Transfer Functions: Application for Wind Retrieval from Spaceborn Scatterometer Data", J. Geophys. Res., Vol. 98, pp. 22,827-22,841
Weng, F., and N.C. Grody, 1994 , "Retrieval of Cloud Liquid Water Using the Special Sensor Microwave Imager (SSM/I)", J. Geophys. Res., Vol. 99, pp. 25,535-25,551
Weng, F., N.C. Grody, R. Ferraro, A. Basist and D. Forsyth, 1997, "Cloud Liquid Water Climatology from the Special Sensor Microwave/Imager", J. of Climate, Vol. 10, pp. 1086-1098
Wentz, F.J., 1992, "Measurement of Oceanic Wind Vector Using Satellite Microwave Radiometers", IEEE Trans. Geosci. Remote Sens., Vol. GE-30, pp. 960-972
Wentz F.J., 1997, "A Well-Calibrated Ocean Algorithm for Special Sensor Microwave / Imager", J. Geophys. Res., Vol. 102, pp. 8703-8718
Yu, T.-W., M.D. Iredell and D. Keyser, 1997, "Global Data assimilation and Forecast Experiments Using SSM/I Wind Speed Data Derived from a Neural Network Algorithm". Weather and Forecasting, Vol. 12, pp . 859-865
Yu, T.-W., and W.-S. Wu, 1999, "Assimilation and Forecast Experiments with SSM/I Wind Speed Data Derived from a Neural Network Algorithm at NCEP" , in Research Activities in Atmospheric and Oceanic Modeling, CAS/JSC Working Group on Numerical Experimentation, WMO/TD, in press
Footnotes:
1. General Sciences Corporation, Laurel, MD 20707
2. The corresponding FORTRAN code is available upon request at: Vladimir.Krasnopolsky@noaa.gov
3. The GSWP algorithm (Petty, 1993) illustrates how to treat the signature of water vapor within the framework of the single-parameter approach.
4. Assuming that all of the other relevant parameters have been identified.
5. Experiments using the OMBNN2 wind speed algorithm have been performed in an operational setting (NCEP's global data assimilation system for May 10 through June 19, 1996) to determine impact. These tests were compared and evaluated against NCEP's operational system which useed the GWS algorithm. Winds speeds generated by OMBNN2 were found to have a more positive impact than the GWS-derived wind speeds, in both the analyses and in forecasts for up to 5 days (Yu et al., 1997).
6. Provided by the Naval Research Laboratory, Washington, D.C.
7. Provided by D. Kilham (Bristol University)
8. The code for the PB retrieval algorithm is based on a detailed published description by Wentz (1997).
9. Positive impact from the assimilation of wind speed and columnar water vapor retrieved by OMBNN3 in an operational numerical weather prediction model is reported by Yu and Wu (1999).
10. Here we switch from m/s to knots, the units which are used by the U. S. maritime industry (1 m/s 2 knots).